| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- 메모이제이션
- 이진탐색
- 깊이 우선 탐색
- linked list
- algorithm
- hash table
- graph
- 비트 연산
- bit manipulation
- CPP
- Sort
- union-find
- Depth-First Search
- binary search
- DFS
- bitwise operation
- 탐욕알고리즘
- dynamic programming
- unordered_map
- Interval
- 동적계획법
- 배열
- binary
- Array
- 알고리즘
- LeetCode
- Greedy
- Sorting
- C++
- 비트 조작
- Today
- Total
공대생 공부노트(Notes for Engineering Studies)
[ leetcode 문제풀이 ] Counting Bits 본문
[ leetcode 문제풀이 ] Counting Bits
301동 노숙자 2022. 1. 16. 03:01
https://leetcode.com/problems/counting-bits/
Counting Bits - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
(Counting Bits 문제는 위 링크에서 풀어보실 수 있습니다.)
< Counting Bits 문제 설명 >
Counting Bits 문제는 다음과 같다.
Given an integer n, return an array ans of length n+1 such that for each i (0 <= i <= n), ans[i] is the number of 1's in the binary representation of i.
주어진 정수 n에 대하여 길이는 n+1이고 i번째 원소가 i의 이진 표현에서 1의 개수에 해당하는 ans 배열을 리턴하여라.
다음 두 가지 출력 예시가 주어졌다.
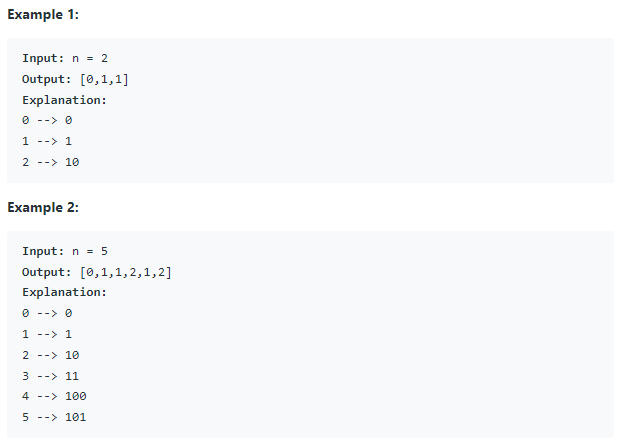
주어진 제한 조건은 0 ≤ n ≤ 10^5이 있고, Follow up question으로는 아래 2개가 있다.
- O(n log n)의 시간복잡도를 가지는 솔루션은 매우 쉽게 구할 수 있다. 그렇다면 선형 시간 내에 (O(n)의 시간복잡도로), 단번에 풀 수 있겠는가?
- built-in 함수를 사용하지 않고 풀 수 있겠는가?
< Counting Bits 문제 접근 - 기본 >
우선 두 가지 출력 예시로부터 리턴해야 하는 배열이 무엇인지, 어떤 것을 의미하는지는 명확하게 알 수 있다. 그렇다면 가장 쉽게 솔루션을 구할 수 있는 방법은 직접 0~n 사이의 정수를 이진표현으로 나타내 1의 개수를 세는 것이다. 이는 다음과 같은 코드로 나타낼 수 있을 것이다. (Cpp 사용)
vector<int> countBits(int n){
vector<int> bitcount;
bitcount.push_back(0); // 반복문의 편의성을 위해 0에 대한 계산 먼저 처리
for(int i=1;i<=n;i++){
int current_num = i;
int cnt = 0;
while(current_num){ // 시프트 연산에 의해 current_num이 0이 될 때까지 반복
cnt+=(current_num%2); // 현재 이진표현 상 가장 오른쪽 숫자가 1일경우 카운트
current_num = (current_num>>1);
}
bitcount.push_back(cnt); // current_num에 해당하는 인덱스에 구한 값(cnt)할당
}
return bitcount;
}이 코드 실행에서의 시간복잡도를 생각해보면 runtime은 for문과 while문에 의해 결정된다.
while문 내에서는 시프트 연산의 반복으로 runtime은 O(log current_num) = O(log n)이며, 이를 총 n회 반복하므로 시간복잡도가 넉넉히 O(n log n)을 만족함을 알 수 있다.
그렇다면 follow up question에서 요구하는 O(n)의 시간복잡도를 만족하기 위해서는 어떻게 해야 할까?
< Counting Bits 문제 접근 - 심화 >
정수의 이진표현에서 1이 어떻게 나타나는지를 우선 확인해보자. (0은 제외)
| 1 = 1 | |||||||
| 2 = 10 | 3 = 11 | ||||||
| 4 = 100 | 5 = 101 | 6 = 110 | 7 = 111 | ||||
| 8 = 1000 | 9 = 1001 | 10 = 1010 | 11 = 1011 | 12 = 1100 | 13 = 1101 | 14 = 1110 | 15 = 1111 |
숫자의 구간을 2^m ~ 2^(m+1)-1 으로 나누어 패턴을 살펴보면 각 숫자를 2로 나눈 몫이 가장 오른쪽 한 자리를 제외한 숫자의 이진표현이 된다. 한편 가장 오른쪽 한자리는 그 숫자의 2로 나눈 나머지로 나타난다. (ex - 11의 경우 2로 나눈 몫 5 = 101과 2로 나눈 나머지 1을 이어붙인 꼴이다.)
이 패턴에 따라 0에서부터 순차적으로 배열 자신의 값을 참조해 솔루션을 구할 수 있다. 이는 아래와 같이 코드로 나타낼 수 있다. (Cpp 사용)
vector<int> countBits(int n) {
vector<int> bitcount;
bitcount.push_back(0); //기본 값으로 0에 대한 값 대입
for(int i=1;i<=n;i++){
bitcount.push_back(bitcount[i/2] + i & 1); //2로 나눈 몫, 나머지 고려
}
return bitcount;
}이 코드의 시간복잡도를 생각해보면, for문 내부에서 처리하는 연산은 상수시간이므로 이를 n회 반복하는 for문에 의해 결정된다. 따라서 시간복잡도는 O(n)으로 최적화 달성에 성공하였다.
'2022 Algorithm Study(by leetcode) > Binary' 카테고리의 다른 글
| [ leetcode 문제풀이 ] Sum of Two Integers (0) | 2022.01.16 |
|---|---|
| [ leetcode 문제풀이 ] Missing Number (0) | 2022.01.16 |
| [ leetcode 문제풀이 ] Reverse Bits (0) | 2022.01.16 |
| [ leetcode 문제풀이 ] Number of 1 Bits (0) | 2022.01.16 |




